Множення чисел на палочках Непера

http://all-ht.ru/inf/history/p_0_12.html

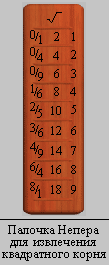
https://www.facebook.com/100009439936966/videos/1997487383909240/

Палочки Непера

В книге, изданной в 1617 году, шотландский ученый Джон Непер описал способ умножения с помощью палочек, который в дальнейшем получил название «Палочки Непера». В основу этого устройства лег принцип умножения решеткой, широко распространенный в XVII веке.

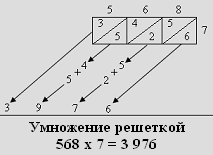
Для умножения решеткой использовалась таблица, содержащая столько столбцов, сколько разрядов у множимого, и столько строк, сколько разрядов у множителя. Над столбцами таблицы записывается множимое так, чтобы разряды числа находились каждый над своим столбцом. Справа от таблицы записывался множитель так, чтобы каждый разряд числа был напротив своей строки. При этом старший разряд записывался напротив верхней строки. В каждую ячейку таблицы записывался результат перемножения разряда множимого, находящегося над этой ячейкой, и разряда множителя, находящегося справа от этой ячейки. Причем для записи результата ячейка разделялась по диагонали на две части. В верхнюю часть записывался старший разряд результата, а в нижнюю – младший. Затем произведения суммировались по наклонным плоскостям справа налево. Полученная сумма и есть окончательный результат. Проиллюстрируем выше сказанное на примере 568 * 7:

1. Чертим решетку с тремя столбцами и одной строкой, разделяем ячейки решетки на две части по диагонали.

2. Умножаем старший разряд множимого на множитель (5*7 = 35) и записываем результат в первую ячейку, причем разряд десяток записываем в верхнюю часть ячейки, а разряд единиц - в нижнюю.

3. Умножаем разряд десятков множимого на множитель (6*7 = 42) и записываем результат во вторую ячейку.

4. Умножаем разряд единиц множимого на множитель (8*7 = 56) и записываем результат в третью ячейку.

5. Суммируем строку решетки по наклонной плоскости справа налево. Суммирование по наклонной плоскости проводится поразрядно с переносом переполнения в старший разряд. Каждый разряд равен сумме чисел в прилегающих друг к другу треугольниках соседних ячеек. Полученная сумма - это результат умножения.

На рисунке слева приведен пример умножения с помощью решетки для многоразрядного множителя. Все действия аналогичны примеру с одноразрядным множителем, только несколько усложняется суммирование по наклонной плоскости.

Используя этот способ умножения, Джон Непер создал свой прибор – «Палочки Непера». Он представлял собой набор палочек, в который входила одна палочка с нанесенными на нее цифрами от 1 до 9 (указатель строк) и палочки с таблицей умножения всех чисел от 1 до 9 (разряды множимого). Сверху каждой такой палочки наносилось число от 1 до 9, а вдоль длины – результаты умножения этого числа на все числа от 1 до 9. По сути дела палочки Непера представляли собой решетку для умножения числа 123456789 на число 123456789, разрезанную на столбцы.

Для умножения с помощью этого прибора выбирались палочки, соответствующие значениям разряда множимого, и выкладывались в ряд так, чтобы цифры сверху каждой палочки составляли множимое. Часто значения разрядов множимого повторялись, поэтому в наборе всегда было несколько палочек для каждого разряда. Слева прикладывали палочку с цифрами от 1 до 9 (указатель строк), по которой выбирали строки, соответствующие разрядам множителя. Затем каждая отобранная строка суммировалась по наклонной плоскости. Полученные результаты складывались между собой с учетом порядка разрядов множителя.

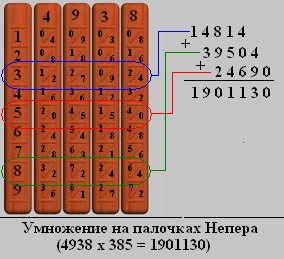
Рассмотрим технику умножения с помощью палочек Непера на примере перемножения чисел 4938 и 385:

1. Выбираем палочки с таблицей умножения чисел 3,4,8 и 9.

2. Выкладываем их вряд так, чтобы цифры сверху каждой палочки составили число 4938.

3. Выкладываем слева указатель строк.

4. Ориентируясь по крайней левой палочке, проводим суммирование по наклонной плоскости для третьей строки. Суммирование проводится по этой строке, так как старший разряд множителя – три. Получаем результат суммирования 14814.

5. Аналогичные действия проводим для восьмой строки, так как второй разряд множителя – восемь. Результат суммирования – 39504.

6. Эти же действия проводим для младшего разряда множителя, которому соответствует пятая строка. Результат суммирования – 24690.

7. Складываем полученные ранее результаты с учетом порядка разрядов множителя. Так как первая сумма вычислялась для разряда сотен, то умножаем ее на 100. Соответственно вторую сумму умножаем на 10, а третью оставляем без изменения. Складываем полученные результаты: 1 481 400 + 395 040 + 24690 = 1 901 130. Полученная сумма и есть результат перемножения чисел 49380 и 385.

Палочки Непера могли использоваться не только для умножения, но и для деления, и излечения квадратного корня. Рассмотрим технику деления на примере 491756 / 3852 = 127.6625:

1. Выбираем палочки с таблицей умножения чисел 2,3,5 и 8.

2. Выкладываем их в ряд так, чтобы цифры сверху каждой палочки составили делитель (3852).

3. Суммируем по наклонной плоскости первый ряд и записываем напротив него результат. Эту же операцию проделываем с оставшимися восемью рядами.

4. Теперь приступаем непосредственно к делению. На этом этапе необходимо найти наибольшее число из столбца сумм, но при этом оно должно быть меньше делимого с учетом разрядности. То есть необходимо привести числа из столбца сумм к единому порядку с делимым и уже из этих чисел выбирать нужное нам. Для нашего примера - это число из первой строки с учетом приведения к единому порядку с делимым 385200. Вычитаем найденное число (385200) из делимого и получаем старший разряд результат и остаток. Старший разряд результата будет 1, так как мы выбрали число из первой строки. Остаток от деления будет 491756 - 385200 = 106556.

5. Повторяем действия, описанные в пункте 4, но применительно к остатку от деления. В результате получаем следующий разряд результата (2) и новый остаток (29516). Повторяем эти действия до тех пор, пока остаток больше делителя. Когда остаток от деления становится меньше делителя, означает, что найдена целая часть результата. В нашем случае это произойдет после трех итераций, и целая часть результата будет 127.

6. Увеличиваем остаток от деления в 10 раз и проводим с ним описанные выше действия, в результате получаем десятые доли результата (для нашего примера 6) и новый остаток. Повторяем эти действия до тех пор, пока не будет достигнута необходимая точность деления или остаток не будет равен нулю.

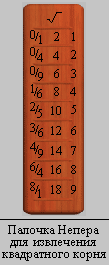
Для извлечения квадратного корня использовалась дополнительная палочка, имеющая три столбца. Первый столбец содержал возведенные в квадрат значения указателя строк. Второй столбец содержал числа, получаемые умножением значения указателя строк на два. Третий столбец содержал числа от 1 до 9. Для того, чтобы понять, как производилось вычисления квадратного корня с помощью палочек Непера, рассмотрим пример извлечения квадратного корня из числа 56349.

Извлечение квадратного корня происходит поэтапно. Число разбивают на группы по 2 цифры, начиная с права, и на каждом этапе оперируют со своей парой цифр. При этом от этапа к этапу к паре чисел присоединяется остаток от извлечения квадратного корня на предыдущем этапе.

Этап 1. Число 56349 разбивается на пары следующим образом: 5 63 49. Извлечение квадратного корня начинается с крайней левой группы, в нашем случае это 5.

Выбираем из первого ряда палочки для деления максимальное число, но меньшее первой группы (пяти). Это будет четыре: 4 < 5 < 9. Так как число 4 находится во втором ряду, то старший разряд результата будет 2.

Определяем остаток от операции над первой группой, отнимая от значения группы (5) выбранное нами число (4). Остаток будет 1 (5-4 = 1). Зная остаток от операции над первой группой, определяем значение для второго этапа извлечения квадратного корня. Путем объединения остатка(1) и второй группы(63) получаем число 163.

Смотрим значение второго столбца палочки для деления во второй строке (4) и выкладываем это число слева от этой палочки, как показано на рисунке «Извлечение кв. корня. Этап 1». Подсчитываем сумму всех рядов по наклонной плоскости, игнорируя второй и третий столбцы палочки, для извлечения квадратного корня и записываем их справа от выложенных палочек.

Этап 2. Выбираем наибольшее число из столбца суммирования строк по наклонной плоскости, которое в свою очередь меньше числа, определенного для второго этапа (163). Это будет 129 (129<163<176) из третей строки. Таким образом, следующий разряд результата будет 3.

Определяем остаток от операции на втором этапе, отнимая от числа, определенного для второго этапа (163), выбранное нами число (129). Остаток будет 34 (163-129 = 34). Зная остаток, определяем значение для третьего этапа извлечения квадратного корня. Путем объединения остатка(34) и третей группы(49) получаем число 3449.

Смотрим значение второго столбца палочки для деления в третьей строке (6) и выкладываем палочку, соответствующую этому числу слева от палочки для деления, как показано на рисунке «Извлечение кв. корня. Этап 2». Подсчитываем сумму всех рядов по наклонной плоскости, игнорируя второй и третий столбцы палочки, для извлечения квадратного корня и записываем их справа от выложенных палочек.

Этап 3. Выбираем наибольшее число из столбца, который получился в результате суммирования строк по наклонной плоскости, которое в свою очередь меньше числа, определенного для третьего этапа (3449). Это будет 3269 (3269<3449<3744) из седьмой строки. Таким образом, очередной разряд результат будет 7.

Определяем остаток от операции, отнимая от числа, определенного для третьего этапа (3449), выбранное нами число (3269). Остаток будет 180 (3449-3269 = 180). Зная остаток, определяем значение для продолжения извлечения квадратного корня на четвертом этапе. Так как для четвертого этапа не осталось группы для объединения с остатком, то разряд результата, полученный после четвертого этапа, будет разряд десятых частей. А для вычисления числа для четвертого этапа остаток (180) объединяется с группой, состоящей из двух нулей (00). Таким образом, число для четвертого этапа будет 18000.

Смотрим значение второго столбца палочки для деления в седьмой строке (14). Объединяем число, выложенное палочками (46), с 14 по следующему правилу: разряд десятков от числа 14 прибавляем к числу выложенными палочками (46+1=47), а разряд единиц просто приписываем справа и получаем 474. Выкладываем это число слева от палочки для извлечения квадратного корня, как показано на рисунке «Извлечение кв. корня. Этап 3». Подсчитываем сумму всех рядов по наклонной плоскости, игнорируя второй и третий столбцы палочки для извлечения квадратного корня, и записываем их справа от выложенных палочек.

Этап 4. Выбираем наибольшее число из столбца суммирования строк по наклонной плоскости, которое меньше числа, определенного для четвертого этапа (18000). Это будет 14229 (14229<18000<18976) из третьей строки. Таким образом, разряд десятых частей результата будет 3. Следовательно, квадратный корень из 56349 будет 237,3…

Далее повторяем действия, описанные в третьем этапе, до тех пор, пока не будет достигнута заданная точность или остаток от операции не будет равен нулю. Если получен нулевой остаток, то это означает, что корень извлекается точно.

Было множество попыток усовершенствовать палочки Непера. Так в 1668 году Каспар Шот предложил вместо брусочков использовать цилиндры, на поверхности каждого из которых нанесены значения всех палочек Непера с таблицей умножения от 1 до 9. Цилиндры помещались в ящик параллельно друг другу. Повернув цилиндры так, чтобы их верхние цифры составляли множитель, можно проводить умножение также, как и с помощью палочек Непера.

В 19 веке для облегчения счета палочки Непера стали делать на брусочках, располагающихся под углом в 65 градусов. Таким образом, треугольники, используемые для сложения, при счете по наклонной плоскости располагались друг под другом.

А в 1892 году был создан прибор для умножения, использующий вместо палочек узкие полоски, закрепленные в футляре в виде записной книжки и передвигающиеся с помощью заостренной палочки.

Палочки Непера были очень популярны и привлекали многих изобретателей. За века их использования было предложено много разнообразных усовершенствований и устройств для их использования. Однако, это было не единственное изобретение Непера, повлиявшее на развитие устройств для счета. Он заложил понятие логарифма и основы логарифмического исчисления, речь о котором пойдет в следующем разделе.