ПРИКЛАДИ НА ВСІ ДІЇ З НАТУРАЛЬНИМИ ЧИСЛАМИ
1A. Обчислити
числові вирази (усі дії записати письмово):
1) А) 2058:(4608:48 – 4465:95)∙101010;
Б) 3332:(4324:46 – 4185:93)∙202020.
Б) 3332:(4324:46 – 4185:93)∙202020.
2) А) 3822:(4048:44 – 3913:91)∙303030;
Б) 2832:(3738:42 – 3668:86)∙404040.
Б) 2832:(3738:42 – 3668:86)∙404040.
3) А) 4753:(3393:39 – 3268:86)∙505050;
Б) 3724:(3145:37 – 3024:84)∙606060.
Б) 3724:(3145:37 – 3024:84)∙606060.
4) А) 4753:(2905:35 – 2788:82)∙707070;
Б) 3328:(2673:33 – 2291:79)∙808080.
Б) 3328:(2673:33 – 2291:79)∙808080.
5) А) 5049:(2184:28 – 2079:77)∙909090;
Б) 4539:(1976:26 – 1875:75)∙100100100.
Б) 4539:(1976:26 – 1875:75)∙100100100.
2B.
Розв’язати
рівняння і виконати перевірку:
1) А) 2058:(4608:х – 4465:95)∙10101 = 424242;
Б)
3332:(4324:46 – 4185:у)∙20202= 1373736.
2) А)
3822:(4048:х – 3913:91)∙30303 =2363634;
Б) 2832:(3738:42 – 3668:у)∙40404=2383836.
3) А)
4753:(3393:х – 3268:86)∙50505 =4898985;
Б) 3724:(3145:37 – 3024:у)∙60606 = 4606056.
4) А)
4753:(2905:х – 2788:82)∙70707 = 6858579;
Б) 3328:(2673:33 – 2291:у)∙80808 = 5171712.
5) А)
5049:(2184:х – 2079:77)∙90909 = 8999991;
Б) 4539:(1976:26 – 1875:у)∙1001001 =89089089.
3C. Знайти
кількість двоцифрових натуральних чисел, що мають у цифрі одиниць тільки цифри:
3, 4, 5.
4D. Знайти
кількість двоцифрових натуральних чисел, що мають у цифрі десятків тільки
цифри: 6, 3, 0, 9.
5E. Знайти
кількість трицифрових натуральних чисел, що містять у цифру 6 або 3.
6F. Знайти
кількість усіх цифр, що містяться в
натуральних числах від 1 до 2014.
Відношення порядку на множині натуральних чисел
Означення. Натуральне число m більше, ніж натуральне число к, якщо існує таке натуральне число n, що
m = к + n.
В даному разі також кажуть,
що к менше, ніж m.
Самі відношення «більше, ніж» та
«менше, ніж» записують відповідно в
такому вигляді:
m > к «число m більше, ніж число
к »
та
к < m «число к менше, ніж число m ».
Відношення порядку має такі
властивості:
1) Для довільних двох
натуральних чисел справджується одне й
лише одне з тверджень: або перше більше, ніж друге, або друге
більше, ніж перше, або вони рівні між собою;
лише одне з тверджень: або перше більше, ніж друге, або друге
більше, ніж перше, або вони рівні між собою;
2) Нехай m>к і к>n, тоді m>n , тобто, якщо
одне число більше, ніж друге, а друге більше, ніж третє, то перше число більше,
ніж третє;
3) Нехай m
> к, тоді m+n > к+n, тобто, до обох частин нерівності можна додавати одне й те саме число зі збереженням знаку нерівності;
4) Нехай m
> к, тоді mn
> кn тобто, обидві частини нерівності можна множити на одне й те
саме натуральне число зі збереженням знаку нерівності.
Зауваження. Легко сформулювати властивості,
аналогічні до трьох останніх, для відношення порядку "менше",
здійснивши формальну заміну >(більше) на <(менше).
Найбільше та найменше
значення числової множини
Якщо деяка непорожня підмножина натурального ряду містить скінчену(обмежену)
кількість чисел, то серед них існує найменше(мінімальне) число цієї підмножини
та найбільше(максимальне) число цієї підмножини.
Означення.
1. Елемент n називають найменший елемент множини М для відношення порядку <, якщо для
усіх елементів m з
М, що нерівні n, справедлива
нерівність n
< m.
Такий елемент, якщо він
існує, позначають так: minМ або
n = min m;
mєМ
2. Елемент n називають найбільший елемент множини М для відношення порядку <, якщо для усіх елементів m з М, що нерівні n, справедлива нерівність m < n.
Такий елемент, якщо він існує, позначають так: mахМ або
n = max m;
mєМ
Зауваження. Найбільшого натурального числа не існує (див. аксіому 2). Якщо для підмножини А натурального ряду існує таке натуральне число, що
більше, ніж будь-який елемент А, то існує найбільший елемент
А.
Зауваження. Будь-яку непорожню підмножину натурального ряду можна впорядковати, тобто, усі числа підмножини можна
записати в порядку зростання від
найменшого до найбільшого.
Будь-яку непорожню підмножину
натурального ряду можна впорядковати, тобто, усі числа
підмножини можна записати в порядку спадання від
найбільшого до найменшого.
Завдання на дослідження властивостей
натуральних чисел.
1. Скільки існує натуральних чисел
від 1 до 1000 включно, у яких сума цифр рівна 24?
Відповідь: 10
чисел: 888, 996, 969, 699, 987, 897, 879, 978, 798, 789.
2. Скільки існує натуральних чисел
від 1 до 1000, у яких сума цифр рівна 3?
Відповідь: 10 чисел: 3, 30, 300, 12, 21, 102, 120, 210,
111, 201.
3. Скільки існує натуральних чисел
від 1 до 1000 включно, у яких сума цифр рівна 1?
Відповідь: 4
чисел: 1, 10, 100, 1000.
4. Чи існує натуральне
десятицифрове число, яке ділиться націло на 11, у запису якого різні цифри?
Відповідь: так,
існує, і не одне. Наприклад: 2753967180 або 1427385960 та інші.
5. Яких двоцифрових чисел більше:
тих, що є добутками двох будь-яких цифр, чи тих, які не дорівнюють добутку двох
цифр?
Відповідь: менше
тих, що є добутками цифр.
6. Яке найменше натуральне число
можна отримати, шляхом розстановки знаків плюс та мінус перед числами 1, 2, 3,
4, 5, …. , 99?
Відповідь: 1.
7. Чи можна у вершинах
рівностороннього восьмикутника розташувати числа 1, 2, 3, 4, 5, 6, 7, 8 таким чином, щоб суми чисел розташовані у
будь-яких трьох сусідніх вершинах були б
більше 11?
Відповідь: Так, наприклад, по часовій
стрілці: 1, 5, 7, 2, 4, 6, 3, 8.
8. Чи існує натуральне число від 1
до 1000, у яке при діленні на 9 має
остачу 2, а при діленні на 6 має остачу 1?
Відповідь: не
існує.
9. Знайти натуральне число, сума
цифр якого дорівнює різниці між числом 328 і
самим числом?
Відповідь: 317.
10. В Іванка 44 монети і 10 кишень.
Чи зможе він розкласти монети в кишені так, щоб в кожній кишені була різна
кількість монет?
Відповідь: не
може.
11. Від двоцифрового числа відняли суму його цифр і отримали число,
записане тими самими цифрами, але в зворотному порядку. Яке це число?
Відповідь: 54.
12. Чи можна у вершинах
рівностороннього восьмикутника розташувати числа 1, 2, 3, 4, 5, 6, 7, 8 таким чином, щоб суми чисел розташовані у
будь-яких трьох сусідніх вершинах були б
більше 13?
13. Відповідь: не можна. Знайти двоцифрове число, перша цифра якого дорівнює різниці
між числом, записаним тими самими цифрами, але в зворотному порядку.
Відповідь:98
14. Знайти двоцифрове число, яке
дорівнює сумі цифри його десятків і квадрату цифри одиниць.
Відповідь:89
15. У трицифровому числі закреслили
середню цифру. Отримане двоцифрове число в 6 разів менше трицифрового. Знайти
трицифрове число.
Відповідь:108
16. Взяли шість 7-цифрових
натуральних чисел. Деякі з них записали як суму із семи доданків. Потім деякі з чисел
знову записали як суму із семи
доданків. І так далі. Після цього
підрахували усі числа, їх виявилось
67. Чи правильно виконаний підрахунок?
Відповідь: не правильно
17. Чи існує квадрат
3х3, в клітинках якого розташовані
натуральні числами від 1 до 3 таким чином, сума
трьох різних цифр: у кожній діагоналі , у кожному стовпчику, у кожному
рядку рівна?
Відповідь: не
існує.
18. Якщо між цифрами деякого
двоцифрового числа вписати 0, то отримаємо трицифрове число, яке в 9 разів
більше від початкового числа. Яке початкове число?
Відповідь: 45.
Ознаки
подільності натуральних чисел.
Ознака подільності натурального числа n на натуральне число k – це твердження, що
залежить від цифрового запису і перевірка істинності якого, особливо для
великих n, потребує менше
обчислень, ніж безпосереднє ділення з остачею n на k. Ознаки подільності різні в різних системах числення. Cформулюємо деякі ознаки подільності у десятковій системі
числення.
Означення. Факторизація або розклад на множники числа — це декомпозиція об'єкту (наприклад, числа, у добуток інших об'єктів(чисел), або множників, які після перемноження дадуть вихідний об'єкт. Наприклад, число 15 розкладається на прості множники як 3 × 5,Метою факторизації є зазвичай звести щось до «базових будівельних блоків», наприклад, цілі числа до простих чисел.
В теорії чисел основна теорема арифметики стверджує, що будь-яке натуральне число більше одиниці може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників.
Таким чином, теоремою стверджується, що не існує таких чисел, які можна було б розкласти на прості множники різними способами.
Нехай натуральне число у десятковій системі числення має вигляд десяткового запису.
В теорії чисел основна теорема арифметики стверджує, що будь-яке натуральне число більше одиниці може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників.
Для знаходження розкладу натурального числа на прості множники послідовно застосовується операція ділення числа на прості числа починаючи з найменшого. Причому, перехід до наступного більшого простого числа виконується тільки при неможливості цілого ділення на менше. Так, наприклад, можна отримати наступні розклади чисел 420 та 1200:
Таким чином, теоремою стверджується, що не існує таких чисел, які можна було б розкласти на прості множники різними способами.
Нехай натуральне число у десятковій системі числення має вигляд десяткового запису.
З основної теореми арифметики можна зробити висновок про важливість простих чисел в арифметіці, на основі яких можна побудувати будь-яке ціле число.
Знаючи розклад числа на прості множники, можна отримати усі його дільники. Будь-який додатний дільник числа буде представлений тим же набором простих чисел, але з меншими показниками степеня у відповідних множників. Так, наприклад, всі дотатні дільники числа 1200 будуть мати наступну форму  де
де  ,
, 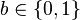 та
та  . Загальна кількість таких дільників буде дорівнювати
. Загальна кількість таких дільників буде дорівнювати  .
. Натуральне число ділиться без остачі на:
·
2,
якщо aо : 2 — остання цифра десяткового запису парна;
·
3,
якщо (an+an-1 + …+ aо): 3
– сума цифр десяткового
запису а ділиться без остачі на 3;
запису а ділиться без остачі на 3;
·
4,
якщо a1aо : 4 – число, утворене двома останніми цифрами
десяткового запису a, ділиться без остачі на 4;
десяткового запису a, ділиться без остачі на 4;
·
5,
якщо aо = 0 або aо = 5 – остання цифра десяткового запису
a дорівнює 0 або 5;
a дорівнює 0 або 5;
·
6,
якщо воно ділиться без остачі на 2 і на 3 одночасно;
·
7,
якщо знакозмінна сума трицифрових чисел:
ділиться без остачі на 7;
·
9,
якщо (an+an-1 + …+ aо): 9 – сума цифр десяткового
·
запису
a ділиться без остачі на 9;
·
10,
якщо aо = 0 – остання цифра десяткового запису a дорівнює нулю;
·
11,
якщо (an-an-1 + …+aк - aк-1 + …- a1 + aо) : 11 – знакозмінна
сума цифр ділиться без остачі на
11;
·
12,
якщо воно ділиться без остачі на 3 і 4;
·
13, якщо знакозмінна сума
трицифрових чисел:
ділиться без остачі на 13.
Прості та
складені числа
Визначення. Натуральне число р називається простим, якщо р > 1
и р не має дільників, відмінних
від 1 і р.
Приклади простих чисел: 2, 3, 5, 7 11, 13, 17, 19, 23,
29, 31, 37, 41, 47, 53, 57, 61, 67, 71, 73, 79, 83, 89, 101, 103, …, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027,
2029 , 2039, 2053, 2063, 2069, 2081, 2083, 2089, 2099, …
Теорема
Евкліда. Простих чисел безліч.
Доведення (від супротивного).
Припустимо, що р1, р2, ... , pn – всі різні прості числа натурального ряду. Тоді всі числа, відмінні від простих дільників, кратні хоча б одному з елементів р1,
р2, ... , рn. Проте таке натуральне число
(р1∙p2 ∙…∙pn + 1) – взаємно просте з усіма цими числами. Отримана суперечність засвідчує хибність припущення
про скінченність множини простих елементів.
Усі
натуральні числа поділяються на три групи:
1 множина –
це одиниця, має тільки один дільник.
2 множина –
це прості числа, які мають тільки по два дільники,
3 множина – це складені числа, які мають більше,
ніж два дільника.
Теорема. Складених чисел
безліч.
Теорема. Довільне
натуральне n
> 1 можна подати у вигляді добутку простих чисел.
Доведення (методом математичної індукції за n).
1. 2 – просте число, тому 2 =
2 – шукане подання для n = 2.
2. Припустимо, що твердження
теореми справджується для всіх
n £ k. Доведемо, що
воно справджується і для n = k + 1.
Можливі два випадки:
1) n = (k + 1) – просте. У даному разі n = n є шуканим розкладанням на множники;
2) n = (k + 1) не є
простим, тобто існують такі натуральні a та b, при яких
n = k+1 = ab, a > 2, b > 2.
З останніх співвідношень
випливає, що a та b не перевищують
(k + 1)∙0,5 і k.
Таким чином, для a і b розкладення на
прості множники існують. Перемноживши відповідні подання на прості множники, отримаємо розкладення на множники для (k + 1).
3. Таким чином, якщо твердження теореми
справджується для всіх натуральних n, що не
перевищують k, то воно справджується і для
всіх натуральних n, які не перевищують (k + 1). На підставі 5-ої аксіоми Пеано робимо висновок
про істинність теореми.
Означення. Розкладання натурального числа на прості множники називають канонічним, якщо прості множники записують у порядку неспадання.
Наприклад, розкладення 21 =
3∙7 – канонічне, а 21 = 7∙3 – не канонічне.
Зауваження. Натуральні числа збігаються тоді й лише тоді, коли
збігаються їхні канонічні розкладення на прості множники.
Доведення зводиться до
аналізу можливості скорочення спільних множників канонічних розкладень на
прості множники.
Кількість дільників
натурального числа
Теорема. Нехай канонічне
розкладення на прості множники натурального числа n має такий
вигляд:
тоді кількість всіх різних
натуральних дільників n дорівнює:
(a1 + 1) ∙ (a2 + 1) ∙…∙ (ak+ 1).
Задачі на дослідження властивостей натуральних
чисел
1. В розкладах на прості множники двох натуральних чисел n та m відсутні
однакові числа. Який спільний дільник
цих чисел? Відповідь: 1.
2. В розкладах
на прості множники двох натуральних
чисел n та m відсутні однакові числа. Яке
спільне кратне(ділене) цих
чисел? Відповідь: nm.
3. В розкладах на прості множники двох
натуральних чисел n та m зустрічаються тільки числа в парних
степенях. Чи являється добуток двох чисел квадратом натурального числа?
Відповідь: Так, цей добуток є квадратом.
4.а Чи може бути квадратом натурального
числа сума квадратів двох непарних чисел? Відповідь: Не може.
4.б Скільки
натуральних дільників має натуральне числа, як отримане піднесенням деякого
простого числа до степеня n? Відповідь: n +1 дільників.
5. Знайти суму цифр n та m, для яких
сума чисел  являється точним квадратом. Відповідь: n + m = 11
являється точним квадратом. Відповідь: n + m = 11
6. Які остачі при діленні на 6 простого числа, більшого ніж 5, можна
отримати? Відповідь: 5 та 1.
7. Чи можна серед натуральних чисел
вигляду n∙ n∙ n∙ n + 4 знайти
просте число? Відповідь: Не можна
8. Чи будь-яке просте число, крім 2 та
3, має вигляд 6к + 1 та 6к -1?
Відповідь: Так.
9. Чи будь-яке
число, що має вигляд 6к + 1 та 6к -1 являється простим?
Відповідь: Не завжди
10. Чи завжди
натуральне число вигляду р∙р -1 (де р – просте число, більше 3) ділиться на 24? Відповідь: Так.
11.
Чи завжди куб натурального числа(не кратного
7) має вигляду 7р -1 або 7р +1 , де р – натуральне число? Відповідь: Так
12.
Чи завжди квадрат натурального число має
вигляд або 5∙р -1, або 5∙р +1, або5∙р,
де р – натуральне число? Відповідь: так
О с н о в н а т е о р е м а
а р и ф м е т и к и.
Для кожного натурального числа n > 1 існує єдиний розклад на прості множники:
n =  , де pi – взаємно прості числа, ki ³ 1 .,
, де pi – взаємно прості числа, ki ³ 1 .,
Розклад являється канонічним.
Приклад. Знайти
всі натуральні числа, що діляться на 6 і мають 35 різних натуральних дільників.
Розв'язання.
6 = 2∙3, тому шукане число ділиться на прості числа 2 і 3. Нехай
2n∙ 3m ∙p3∙
p4 ∙…∙pk –
канонічне розкладення на
прості множники шуканого числа. Тоді, за умовою
задачі, маємо:
(n + 1) ∙ (m + 1) ∙ (k+ 1) ∙ … ∙ (r + 1) =
5 ∙ 7 = 35.
В останній рівності ліворуч
перші два множники більші, ніж 1, а праворуч – добуток двох простих чисел.
Отже, шукане число не має простих дільників, відмінних від 2 чи 3. Таким чином:
n1+1 = 5, m1 +1 = 7, звідси n1= 4, m1 =6.
n2
+1 = 7, m2 +1 = 5, звідси
n2 = 6, m2 = 4.
Відповідь. 24 ∙ 36
або 26 ∙34.
 ,
, 
Означення. Розбиттям числа називається задача представлення натурального числа n у вигляді n = a * b, де a, b – натуральні числа, більші за 1 (не обов’язково прості).
Метод Ферма
Нехай n – складене число, яке не є степенем простого числа. Метод Ферма намагається знати такі натуральні x та y, що n = x2 – y2. Після чого дільниками числа n будуть a = x – y та b = x + y: n = a * b = (x – y)(x + y).
Якщо припустити що n = a * b, то в якості x та y (таких що n = x2 – y2) можна обрати
Приклад. Виберемо n = 143 = 11 * 13.
Тоді x = (13 + 11) / 2 = 12, y = (13 – 11) / 2 = 1.
Найбільший спільний дільник натуральних чисел
Означення. 1) Спільним дільником натуральних чисел а1, а2,
..., аn називається натуральне число d, таке, що a1 : d, а2 : d, ..., аn : d.
2) Найбільшим спільним дільником натуральних чисел а1, а2, ..., аn називається такий спільний
дільник дільник чисел а1, а2,
..., аn, який ділиться на довільний другий спільний
дільник цих чисел.
Найбільший спільний дільник цілих чисел
а
і b можна знайти за допомогою алгоритму Евклида, в основі якого лежить теорема про ділення з остачею. Остання, відмінна від нуля, остача і буде найбольшим спільним дільником чисел а и b.
Означення. Два числа називаються взаємно простими, якщо
найбільший спільний дільник у цих чисел дорівнює одиниці.
Наприклад,
числа 4 та 45 взаємно прості, проте числа 4 та 8 не взаємно прості.
Приклад. Знайти НСД
чисел 1173 и 323.
Послідовним діленням
знаходимо:
1173 = 323´3 + 204;
323=204´1+119;
204=119´1+85;
119=85´1+34;
34=17´2;
так що НСД(1173, 323) = 17.
Зауваження. Зрозуміло, що взаємно простими числами є а і b, якщо їхній найбільший
спільний дільник дорівнює одиниці: НСД(а, b) = 1, тобто, коли існують такі х та у,
для яких
ах + bу = 1,
це згідно алгоритму Евкліда.
Властивості взаємно
простих чисел.
1) Якщо а та b взаємно прості з с,
то добуток аb також
взаємно простий з с.
2) Якщо аb ділиться без остачі на с, що взаємно просте з а,
то b ділиться без остачі на с.
3) Якщо с ділиться на а і b, що взаємно прості, то с ділиться й на добуток аb.
Найменше спільне
кратне натуральних чисел
Означення. Найменшим спільним кратним натуральних чисел а1, а2, ..., аn, відмінних
від нуля, називається найменьше число, кратне всім цим числам.
Обозначают: m=НСК[ а1, а2, ..., аn].
Нехай а и b цілі числа, тоді
НСК
Приклад. Знайти HСK чисел 1173 и 323.
Знаходимо НСД (1173, 323) = 17, тоді
НСК[1173, 323] =
Проблемне запитання: Чи можна будь-яке натуральне, число
більше 4, записати як суму двох простих чисел?
Задачі для самостійного осмислення учнями:
1. Якщо розділити число на
12, отримаємо різницю семи та цього числа. Яке це число?
2. Чи існують двоцифрові
числа, які дорівняють різниці квадратів своїх цифр?
3. Доведіть, що добуток цифр багатоцифрового числа менший
від самого числа.
4. Якщо від задуманого тризначного числа відняти 9, то
одержане число поділиться на 9; якщо від того ж задуманого числа відняти 10, то
результат поділиться на 10, а якщо відняти 11, то результат поділиться на 11.
Знайдіть задумане число.
5. Написали підряд два рази
трицифрове число. Чому утворене число обов’язково поділиться на 7, на 11, 13?
Відповідь: 1001∙аbc = 7∙11∙13∙abc.
6. Від двоцифрового числа
відняли суму його цифр, одержали число, але записане тими самими цифрами, але у
зворотному порядку. Яке початкове число?
Відповідь:
54.
7. У двоцифровому числі число десятків у 2 рази
менше від числа одиниць. Якщо від цього числа відняти суму його цифр, то
дістанемо 18. знайдіть це число.
Відповідь: 24.
8. Двоцифрове число в сумі з числом, записаним
тими самими цифрами, але в зворотному порядку, дає квадрат натурального числа.
Знайдіть всі такі двоцифрові числа.
Відповідь:
29, 38, 47, 56, 65, 74, 83, 92.
9. Якщо першу цифру трицифрового числа збільшити
на n, а другу і третю цифри зменшити
на n, то одержане число буде в n разів більше від
шуканого. Знайдіть це число.
10.
Відповідь: 178.
11.
Цифри трицифрового числа записали в зворотному порядку і
від більшого відняли менше. Доведіть, що різниця цих чисел ділиться на 9.
12.
Доведіть, що сума кубів трьох послідовних натуральних
чисел ділиться на 9. Скільки можна скласти ланцюжків, маючи два блакитних
кільця і три жовтих кільця, якщо кожний ланцюжок може містити тільки 5 кілець? Відповідь
10.
13.
На фермі 1000
голів тварин(кролів та кур). У них 3150 лап. Кого більше на фермі чотирилапих
чи дволапих тварин на фермі. Відповідь:
575 кролів та 425 кур.
14.
Третина п’ятої частини деякого числа менша від третьої
частини цього числа на 60. Знайти це число.
Відповідь: 225.
Задачі на дослідження та осмислення
властивостей
натуральних чисел
1. Чому
дорівнює найменше спільне кратне трьох
послідовних простих чисел? Відповідь: добутку
цих чисел.
2. Чи вірно що
НСД(n; n + m) = НСД(n; m)? Відповідь: так, вірно
завжди.
3. Чи вірно що
НСД(n; n - m) = НСД(n; m)? Відповідь: Так, вірно
завжди.
4. Відомо, що натуральне число вигляду n + 4m ділиться на
13. Чи поділиться на 13 натуральне число
вигляду 10n + m? Відповідь: Так, завжди
поділиться.
5. Відомо, що натуральне число вигляду 3n + 2m ділиться на
17. Чи поділиться на 17 натуральне число
вигляду 10n + m? Так, завжди
поділиться.
6. Який найбільший спільний дільник двох
чисел 2n + 1 та 2n – 1? Відповідь: 1.
7. Чи можна серед натуральних чисел
вигляду (n+1)(n+2)(n+3)n знайти числа, які не діляться на 24?
Відповідь: Ні.
3. Чи числа вигляду 10000…..0001, де
кількість нулів парна, діляться на 11 націло? Відповідь: Так.
4. При яких натуральних n число
вигляду 3n-1 являється
точним квадратом натурального числа? Відповідь: Ці числа не являються
квадратами
5. При яких натуральних n число
вигляду 5n-2 та 5n+2 являється точним квадратом натурального
числа? Відповідь: Ці числа не являються квадратами.
6. При яких натуральних n число
вигляду 7n+3 та 7n-1, 7n-2 являється
точним квадратом натурального
числа?







Немає коментарів:
Дописати коментар